Problem:
Solution:
Disclaimer, I thought about the solution with the hint from wikipedia, in particular, this spinning model. But not the hint text in the problem.
There I started to think, maybe the lines are just joining points on the circle with a phase shift. So I tried:
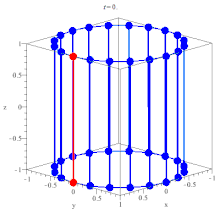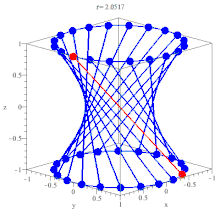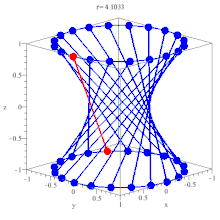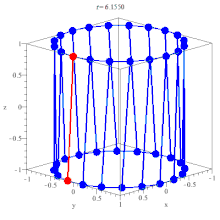
$ (0, 0, -1) \to (\cos \theta, \sin \theta, 1) $, the mid point is $ \frac{1}{2}(\cos \theta, \sin\theta, 0) $, so that is indeed on a circle in the $ z = 0 $ plane.
With that in mind, now I generalize, for the general hyperboloid, when $ z = \pm c $, it is a ellipse with major radius $ \sqrt{2} a $ and minor radius $ \sqrt{2} b $.
Consider the 'phase shift' lines:
$ \sqrt{2}((a \cos u, b \sin u, -c) + v(a \cos (u + s), b \sin (u + s), c)) $
Our goal is to find the unknown $ s $, the phase shift required, to fit the formula. To do that, we just check if all these points is in fact on the hyperboloid.
$ \begin{eqnarray*} & & \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} \\ &=& \frac{(\sqrt{2}(a\cos u + va\cos(u + s)))^2}{a^2} + \frac{\sqrt{2}(b\sin u + vb\sin(u + s)))^2}{b^2} - \frac{(\sqrt{2}((-c) + vc)^2}{c^2} \\ &=& 2(\cos u + v\cos(u + s))^2 + 2(\sin u + v\sin(u + s))^2 - 2(v - 1)^2 \\ &=& 2\cos^2 u + 4v \cos u \cos(u + s) + 2v^2\cos^2(u + s) + 2\sin^2 u + 4v \sin u \sin(u + s) + 2v^2\sin^2(u + s) - 2v^2 + 4v - 2 \\ &=& 2\cos^2 u + 2\sin^2 u + 2v^2\cos^2(u + s) + 2v^2\sin^2(u + s) + 4v \cos u \cos(u + s) + 4v \sin u \sin(u + s) - 2v^2 + 4v - 2 \\ &=& 2\ + 2v^2 + 4v \cos (s) - 2v^2 + 4v - 2 \\ &=& 4v \cos (s) + 4v \\ \end{eqnarray*} $
At this point it should be obvious that $ s = \pm \pi $, that correspond to the two ruling patch for the surface, and the surface is doubly ruled.
Now looking at the hint in the text, I think I can simplify this by making the ellipse at $ z = 0 $ the directix instead, to do so, we just move $ v $ by 1 as follow:
$ \sqrt{2}((a \cos u, b \sin u, -c) + 1(a \cos (u + s), b \sin (u + s), c) + v(a \cos (u + s), b \sin (u + s), c)) $
$ \sqrt{2}((a (\cos u + \cos (u + s)), b (\sin u +\sin (u + s)), 0) + v(a \cos (u + s), b \sin (u + s), c)) $
Now we can use the sum to product formula to simplify this to:
$ \sqrt{2}((a (2\cos(u + \frac{s}{2})\cos \frac{s}{2}), b (2\sin(u + \frac{s}{2})\cos \frac{s}{2}), 0) + v(a \cos (u + s), b \sin (u + s), c)) $
Remember $ s = \pm \pi $, so all these simplifies to simply:
$ (a \cos(u + \frac{s}{2}), b \sin(u + \frac{s}{2}), 0) + v(a \cos (u + s), b \sin (u + s), c) $
Just shift the definition of $ u $ by $ \frac{s}{2} $, we get
$ (a \cos(u), b \sin(u), 0) + v(a \cos (u + \frac{s}{2}), b \sin (u + \frac{s}{2}), c) $
So finally we have these two ruling patches:
$ (a \cos(u), b \sin(u), 0) + v(-a \sin u, b \cos u, c) $
$ (a \cos(u), b \sin(u), 0) + v(a \sin u, -b \cos u, c) $
Now we get back to the full circle to the problem text hint!
Solution:
Disclaimer, I thought about the solution with the hint from wikipedia, in particular, this spinning model. But not the hint text in the problem.
There I started to think, maybe the lines are just joining points on the circle with a phase shift. So I tried:
$ (0, 0, -1) \to (\cos \theta, \sin \theta, 1) $, the mid point is $ \frac{1}{2}(\cos \theta, \sin\theta, 0) $, so that is indeed on a circle in the $ z = 0 $ plane.
With that in mind, now I generalize, for the general hyperboloid, when $ z = \pm c $, it is a ellipse with major radius $ \sqrt{2} a $ and minor radius $ \sqrt{2} b $.
Consider the 'phase shift' lines:
$ \sqrt{2}((a \cos u, b \sin u, -c) + v(a \cos (u + s), b \sin (u + s), c)) $
Our goal is to find the unknown $ s $, the phase shift required, to fit the formula. To do that, we just check if all these points is in fact on the hyperboloid.
$ \begin{eqnarray*} & & \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} \\ &=& \frac{(\sqrt{2}(a\cos u + va\cos(u + s)))^2}{a^2} + \frac{\sqrt{2}(b\sin u + vb\sin(u + s)))^2}{b^2} - \frac{(\sqrt{2}((-c) + vc)^2}{c^2} \\ &=& 2(\cos u + v\cos(u + s))^2 + 2(\sin u + v\sin(u + s))^2 - 2(v - 1)^2 \\ &=& 2\cos^2 u + 4v \cos u \cos(u + s) + 2v^2\cos^2(u + s) + 2\sin^2 u + 4v \sin u \sin(u + s) + 2v^2\sin^2(u + s) - 2v^2 + 4v - 2 \\ &=& 2\cos^2 u + 2\sin^2 u + 2v^2\cos^2(u + s) + 2v^2\sin^2(u + s) + 4v \cos u \cos(u + s) + 4v \sin u \sin(u + s) - 2v^2 + 4v - 2 \\ &=& 2\ + 2v^2 + 4v \cos (s) - 2v^2 + 4v - 2 \\ &=& 4v \cos (s) + 4v \\ \end{eqnarray*} $
At this point it should be obvious that $ s = \pm \pi $, that correspond to the two ruling patch for the surface, and the surface is doubly ruled.
Now looking at the hint in the text, I think I can simplify this by making the ellipse at $ z = 0 $ the directix instead, to do so, we just move $ v $ by 1 as follow:
$ \sqrt{2}((a \cos u, b \sin u, -c) + 1(a \cos (u + s), b \sin (u + s), c) + v(a \cos (u + s), b \sin (u + s), c)) $
$ \sqrt{2}((a (\cos u + \cos (u + s)), b (\sin u +\sin (u + s)), 0) + v(a \cos (u + s), b \sin (u + s), c)) $
Now we can use the sum to product formula to simplify this to:
$ \sqrt{2}((a (2\cos(u + \frac{s}{2})\cos \frac{s}{2}), b (2\sin(u + \frac{s}{2})\cos \frac{s}{2}), 0) + v(a \cos (u + s), b \sin (u + s), c)) $
Remember $ s = \pm \pi $, so all these simplifies to simply:
$ (a \cos(u + \frac{s}{2}), b \sin(u + \frac{s}{2}), 0) + v(a \cos (u + s), b \sin (u + s), c) $
Just shift the definition of $ u $ by $ \frac{s}{2} $, we get
$ (a \cos(u), b \sin(u), 0) + v(a \cos (u + \frac{s}{2}), b \sin (u + \frac{s}{2}), c) $
So finally we have these two ruling patches:
$ (a \cos(u), b \sin(u), 0) + v(-a \sin u, b \cos u, c) $
$ (a \cos(u), b \sin(u), 0) + v(a \sin u, -b \cos u, c) $
Now we get back to the full circle to the problem text hint!


No comments:
Post a Comment