Introduction to Biochemistry - Quiz 2.4.3

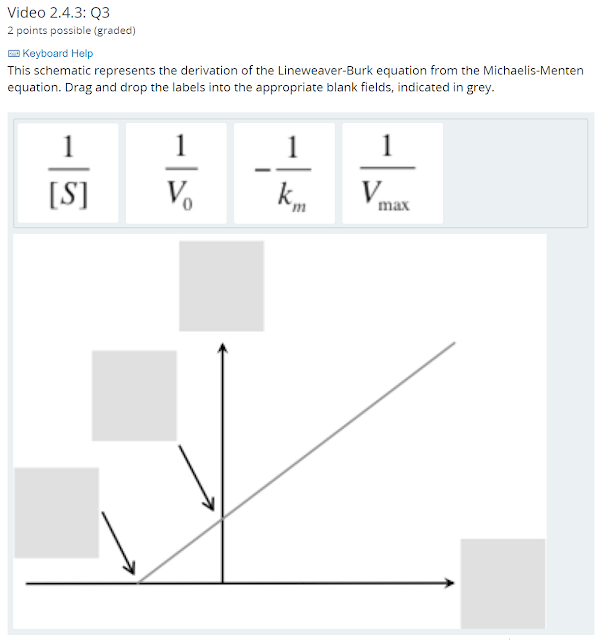
$\begin{eqnarray*} v_0 &=& \frac{v_{max}[S]}{k_m + [S]} \\ \frac{1}{v_0} &=& \frac{k_m + [S]}{v_{max}[S]} \\ \frac{1}{v_0} &=& \frac{k_m}{v_{max}[S]} + \frac{[S]}{v_{max}[S]} \\ \frac{1}{v_0} &=& \left(\frac{k_m}{v_{max}}\right)\left(\frac{1}{[S]}\right) + \frac{1}{v_{max}} \\ \end{eqnarray*}$

It is easier to fit a line than to fit a hyperbola. This plot allow us to get more accurate estimate of $k_m$ and $V_{max}$, and also to plot kinetic data as a line instead of a hyperbolic curve.

Note that while we can visualize $\frac{1}{V_{max}}$ and $\frac{1}{k_m}$ on the line, it is not counted as "directly" visualize $V_{max}$ and $k_m$, therefore the first option is not correct.

The x axis is $\frac{1}{[S]}$
The y axis is $\frac{1}{V_0}$
The y-intercept is $\frac{1}{V_{max}}$
The x-intercept is $-\frac{1}{K_m}$

$V_{max} = \frac{1}{3 \times 10^7} = 3.33 \times 10^{-8} = 33.33 \times 10^{-9} \frac{mol}{L min}$.

$V_{max} = \frac{1}{5 \times 10^4} = 2 \times 10^{-5} = 20 \times 10^{-6} \frac{mol}{L}$.