- Free Energy
- Transition state
- $ \delta G $ uncatalyzed
- $ \delta G $ catalyzed
- Substrate
- ES
- EP
- Product
Technically, I think the answer for 3 and 4 should be the activation energy, not the $ \delta G $, but those are the only given choice, so that's it.
I failed this one. I got this right:
They correctly position the substrate in the active site
But I missed this one
They decrease the entropy of the system.
With bonds, there is reduced randomness, I get that, but how can that contribute the catalysis, I still don't know.
I failed this one too, here is the correct answer:
In Emil Fisher's 'lock-and-key' model of enzyme specificity, the enzyme binds tightly and precisely to the substrate. (That I am correct)
In the modern 'induced fit' model, the enzyme binds weakly to the substrate and then change conformation and binds tightly to the transition state.
My concept was wrong, the enzyme does not binds weakly to the transition state and then change conformation and binds tightly to the product. I was dumb, if it binds tightly to the product, how does it release it?
I feel fairly frustrated at this point, but things are changing ... I got all the rest correct!
If enzyme binds to S1 first, the S1 would probably react with something else. Therefore, the catalysis is more efficient if the enzyme binds S2 first, then change conformation to bind S1, that gives a better chance for S1 to react with S2 since it will be right there.
The answers are:
To measure forward velocity of the reaction with a negligible contribution from the reverse reaction, and
to measure the velocity of the reaction with a known substrate concentration.
Option 3 is bogus, there is no uncatalyzed reaction going on.
Option 4 is also wrong, enzyme we not destroyed.
This is just math. It $ K_m $ is small, then $ [ES] $ is large, the enzyme substrate complex is preferred to the enzyme and the substrate alone, therefore the enzyme has high affinity to the substrate. The reverse it obvious, if $ K_m $ is large, $ [ES] $ is small, the enzyme substrate complex is not preferred to the enzyme and the substrate alone, so the enzyme has a low affinity for its substrate.
This is also just math, if $ [S] $ is way less than $ K_m $, then the denominator is essentially constant even when $ [S] $ change, therefore the answer is
The $ [S] $ term in the denominator is negligible compared to $ K_m $. There is a linear relationship between substrate concentration and velocity.
The question capture above is already filled with answer, it is probably easiest for me to just capture the answer, the original question is just a few in the blank of the derivation.
Answer
This is a graph of uncompetitive inhibitor.
A noncompetitive inhibitor decrease $ V_{max} $ while keeping the $ k_m $ constant, so the first three options are all wrong. It done so by binding both to the enzyme and the enzyme-substrate complex.
Notice $ v_{max} $ is unchanged, this is a competitive inhibitor.











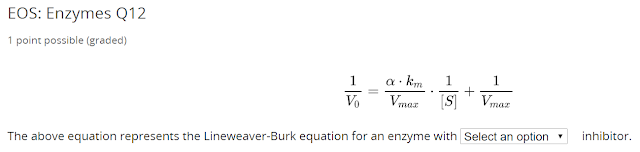
No comments:
Post a Comment