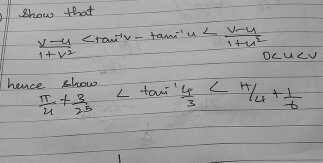Exercise from Quora

Problem:

Please find the problem here.

Solution:

$\begin{eqnarray*} (0! + 0! + 0!)! &=& 6 \\ (1 + 1 + 1)! &=& 6 \\ 2 + 2 + 2 &=& 6 \\ (3 + 3 - 3)! &=& 6 \\ (4 - 4 / 4)! &=& 6 \\ 5 + 5 / 5 &=& 6 \\ 6 + 6 - 6 &=& 6 \\ 7 - 7 / 7 &=& 6 \\ (\sqrt{8 + 8 / 8})! &=& 6 \\ (\sqrt{9 + 9 - 9})! &=& 6 \end{eqnarray*} $

Exercise from 9gag.com?

Problem:

http://9gag.com/gag/aVDxn1O

Solution:

Denote bottle by $ b $

$ b + b + b = 30 $, therefore $ b = 10 $.

Denote the hamburger by $ h $

$ b + h + h = 20 $, therefore $ h = 5 $

Denote the beer by $ e $

$ h + e + e = 9 $, therefore $ e = 2 $.

Now here is the fun

$ \int\limits_{2h - b}^{\infty}{\frac{b\sin x}{ex}dx} = \int\limits_{0}^{\infty}{\frac{10\sin x}{2x}dx} = 5\int\limits_{0}^{\infty}{\frac{\sin x}{x}dx} = \frac{5\pi}{2} $

The last integral is well known, for example, see:
http://math.stackexchange.com/questions/5248/solving-the-integral-int-0-infty-frac-sinxx-dx-frac-pi2

This video explains the Feynman trick!
https://www.youtube.com/watch?v=3LsXWPzlOhQ

Have fun!

Mathematical Analysis - Exercise 1.3

Problem:

Solution:

Suppose $ n = ab $ is not prime, then we can write $ 2^{ab} = (2^{a})^b $. Applying the identity we just proved in the previous problem, we have:

$ 2^{ab} - 1 =  (2^{a})^b - 1 =  (2^{a})^b - 1^b = (2^a - 1)(\cdots) $.

Therefore if $ a \ne 1 $, we have a non-trivial factor for $ 2^{ab} - 1 $.

The contradiction show $ n $ has to be prime.

Mathematical Analysis - Exercise 1.2

Problem:

Solution:

The right hand side sounds like something we can telescope, let's see:

$ \begin{eqnarray*} & & (a - b)\sum\limits_{k = 0}^{n-1}{a^{k}b^{n-1-k}} \\ &=& a\sum\limits_{k = 0}^{n-1}{a^{k}b^{n-1-k}} - b\sum\limits_{k = 0}^{n-1}{a^{k}b^{n-1-k}} \\ &=& \sum\limits_{k = 0}^{n-1}{a^{k+1}b^{n-1-k}} - \sum\limits_{k = 0}^{n-1}{a^{k}b^{n-k}} \\ &=& (a^n + \sum\limits_{k = 0}^{n-2}{a^{k+1}b^{n-1-k}}) - (\sum\limits_{k = 1}^{n-1}{a^{k}b^{n-k}} + b^n ) \\ &=& (a^n + \sum\limits_{k = 1}^{n-1}{a^{k}b^{n-k}}) - (\sum\limits_{k = 1}^{n-1}{a^{k}b^{n-k}} + b^n ) \\ &=& a^n - b^n \end{eqnarray*} $

Mathematical Analysis - Exercise 1.1

Problem:

Solution:

Suppose there exists a largest prime, that means there is only finite number of primes. Consider the product of them plus 1. This number cannot be a prime number because it is larger than the largest prime.

Now consider its prime factorization. Note that when this number is divided by any prime, the remainder 1, therefore, there is just no way of prime factorizing it, contradicting the fundamental theorem of arithmetic, therefore there is no largest prime!

An exercise about Lagrange mean value theorem

Problem:

Solution:

This is a really bored after lunch hour, so I decided let's do a simple calculus exercise to wake my brain up.

The $ \frac{1}{1 + u^2} $ reminded me this has something to do with $ \tan $. So let's do this simple integration.

$ \int{\frac{du}{1+u^2}} = \int{\frac{\sec^2\theta d\theta}{1+\tan^2 \theta}} = \int{d\theta} = \theta = \tan^{-1}u $.

That's refresh my memory! $ \frac{1}{1 + u^2} $ is the derivative of $ \tan^{-1} u $.

Now we apply the Lagrange's mean value theorem to get:

$ \frac{\tan^{-1}v - \tan^{-1}u}{v - u} = \frac{1}{1 + \delta^2} $.

Where $ u < \delta < v $.

$ \tan^{-1}v - \tan^{-1}u= \frac{v - u}{1 + \delta^2} $.

Therefore we conclude (remember when you increase the denominator, the value decrease, and vice versa):

$ \frac{v-u}{1 + v^2} < \tan^{-1}v - \tan^{-1}u< \frac{v - u}{1 + u^2} $.

Last but not least, set $ u = 1 $ and $ v = \frac{4}{3} $ gives

$ \frac{\frac{4}{3}-1}{1 + \left(\frac{4}{3}\right)^2} < \tan^{-1}\frac{4}{3} - \tan^{-1}1< \frac{\frac{4}{3}-1}{1 + 1^2} $.

$ \frac{3}{25} < \tan^{-1}\frac{4}{3} - \tan^{-1}1< \frac{1}{6} $.

$ \frac{\pi}{4} + \frac{3}{25} < \tan^{-1}\frac{4}{3} < \frac{\pi}{4} + \frac{1}{6} $.

Minimizing sum of distances

Problem:

Find $ m $ such that $ \sum_{i = 1}^{n}{\left|x_i - n\right|} $ is minimized.

Solution:

The reaction is that the mean is going to minimize it, but it isn't true. The median will.

Consider a random $ m $, suppose there are $ a $ numbers in $ x_i $ are less than $ m $ and $ b $ numbers of $ x_i $ are larger than $ m $.

If we decrease $ m $ by 1, we change the sum by $ b - a $.
If we increase $ m $ by 1, we change the sum by $ a - b $.

Therefore, as long as $ a \ne b $, we can always reduce the sum, therefore, the only reasonable answer is the median.

This is for the case of odd number of elements, in case we have even number of element, any number between the two center elements would give the same minimal distance sum.

Thanks Sven for generalizing the problem, and Noah for the idea about median.

Some learning in algebraic number theory

Recently I have been reading about proving the algebraic integers form a ring, so let me get started about some simple definitions.

A field is called a number field if it contains $ \mathbf{Q} $.

A number if called an algebraic integer for a number field $ A $ if it can be written as a root of a monic polynomial in $ A $ with coefficient in $ \mathbf{Z} $.

The fact that the algebraic integer form a ring is surprising (to me), it is obvious that $ \sqrt{2} $ and $ \sqrt{3} $ are algebraic integer in $ Q(\sqrt{2}, \sqrt{3}) $, but why $ \sqrt{2} + \sqrt{3} $ an algebraic integer, or in other words, what is the monic polynomial that give root $ \sqrt{2} + \sqrt{3} $?

Turn out the key idea is this polynomial:

$ (x - \sqrt{2} - \sqrt{3})(x - \sqrt{2} + \sqrt{3})(x + \sqrt{2} - \sqrt{3})(x + \sqrt{2} + \sqrt{3}) $.

Obviously, this polynomial is monic and has $ \sqrt{2} + \sqrt{3} $ as a root, but is it in integer, the answer is YES! If we expand this thing, it becomes:

$ x^4 - 10x + 1 $

To verify that, we can put this in wolfram, and wolfram solve the solution as $ \pm\sqrt{5 \pm \sqrt{6}} $, does this value sound familiar. If you read my post about denesting the radical you can just recognize this is basically $ \pm \sqrt{2} \pm \sqrt{3} $

So we have some luck? No, turn out this trick will ALWAYS work because of the theory of symmetric polynomial.

Consider for a moment that we replace square root by variables instead, we have something like this.

$ (x - a_1 - b_1)(x - a_1 - b_2)(x - a_2 - b_1)(x - a_2 - b_2) $

Expanding this thing is messy, so we will not do that, the key idea is that we can consider this as a multi-variable polynomial in $ a_1 $ and $ a_2 $, and more importantly, it is symmetric, such that swapping $ a_1 $ and $ a_2 $ does not change the polynomial itself. Notice the $ x $ and the $ b $ are not going away, we are simply considering them as coefficients by now.

By the theorem of symmetric polynomial, we can rewrite this polynomial as a polynomial of the elementary symmetric polynomial, and viola, because the value of elementary symmetric polynomial is basically the coefficients of the minimal polynomial, they are integers. After substituting the equation with the value of $ a $, we get an expression with integer coefficients of $ X $ and $ b $.

We do the same thing to the $ b $ and finally we get an integer polynomial equation in $ X $ containing the root we wanted!

Conditional Probability

Problem:

Suppose a family has 2 children, one of which is a boy. What is the probability that both children are boys?

Solution:

The reaction is $ \frac{1}{2} $, but that is wrong.

Let the event $ A $ be the event that we have one boy, that event should be $ { BB, BG, GB } $, this event has probability $ \frac{3}{4} $.

Let the event $ B $ be the event that we have two boy, that event should be $ { BB } $, this event has probability $ \frac{1}{4} $.

By the definition of conditional probability, we have:

$ P(B|A) = \frac{P(AB)}{P(A)} =  \frac{P(B)}{P(A)} = \frac{\frac{1}{4}}{\frac{3}{4}} = \frac{1}{3} $.

Rectangles with integer dimensions

Problem:

Find all rectangles with integer dimensions such that its perimeter is equals to its area.

Solution:

Let the length and width of the rectangle be $ x $ and $ y $ respectively. We have

$ 2(x + y) = xy $

Of course, subject to the constraints that $ x \ge 0 $, $ y \ge 0 $, $ x, y \in \mathbf{Z} $.

The key idea is to factorize this as follow:

$ xy - 2x - 2y + 4 = 4 $
$ (x - 2)(y - 2) = 4 $

Once we have that, we know there are only a handful of integer factorization of 4, and we can now check:

$ (x - 2) = 1, (y - 2) = 4 $ gives $ x = 3 $, $ y = 6 $
$ (x - 2) = 2, (y - 2) = 2 $ gives $ x = 4 $, $ y = 4 $

So there we go, there are only two rectangles that satisfy the requirements.

Coursera Coursera Introduction to Physiology - Week 1 - Homeostasis and Endocrine System Exam

1. Even though no food had entered her stomach, the smell and sight of food caused Jane’s stomach to secrete more acid. This is an example of:

feed-forward control

antagonistic control

negative control

tonic control

2. Jerry is a normal 24 year old male with an intracellular fluid (ICF) volume of 24 L. What is the volume of his plasma?

3L

12 L

6 L

9 L

Remember ECF is $ \frac{1}{3} $ and ICF is $ \frac{2}{3} $, so ECF is half of ICF and is therefore $ 12 $. Plasma is $ \frac{1}{4} $ of ECF and is therefore 3 liters.

3. In a normal female, plasma levels of the hormone cortisol are highest in the early morning and half maximal at 4:00 in the afternoon. This is an example of:

circadian rhythm

tonic control

antagonistic control

autocrine control

4. Estrogen acts in the breast to increase the growth of the glands and the number of estrogen receptors in these cells. This is an example of:

antagonistic control

positive feedback

negative feedback

tonic control

5. Potassium ions in the _____ are in equilibrium with potassium ions in the _____.

IVF; ICF

ECF; ICF

IVF; ISF

ISF; ICF

The channel between the IVF and ISF is leaky.

6. A membrane that is permeable only to water separates two solutions of glucose dissolved in water. On one side (A) the glucose concentration is 0.1 g/ml. On the other side (B) the glucose is concentration is 0.6 g/ml. Initially the rate of water flow is:

zero (no flow in either direction)

more rapid from side B to side A

more rapid from side A to side B

the same in both directions

The concentration of water in action again.

7.  Larry drank 2 cups of hypotonic soup. How did the water in the soup distribute into the intracellular (ICF) and extracellular (ECF) compartments?

net water movement from ICF to ECF but less than that seen with isotonic fluid ingestion.

net water movement from ECF to ICF greater than that seen with isotonic fluid ingestion.

no change in water distribution between ICF and ECF.

water will distribute equally (1/2 and 1/2) between ICF and ECF.

Remember hypotonic soup means its solute is less concentrated than 300 mOsM. Therefore the concentration of water is higher than ICF, and therefore more water going into ICF.

8. The single most important factor that determines whether a given cell can be regulated by the steroid hormone aldosterone is the presence in this cell of:

specific aldosterone receptors

heat shock proteins

cAMP and ADP

active transporters for aldosterone

9. In obesity related Type II diabetes, levels of the peptide hormone, insulin, are either normal or elevated, yet target cells are less sensitive to the binding of insulin. This suggests that the target cells:

have excess intracellular glucose

are impermeable to insulin

have a defect in their receptor signaling pathway

cannot convert insulin to an active form

10. What is the maximum transport rate (Tm ) of the carrier depicted below?

8

10

20

4

11. When steroid hormones bind to their target cell receptors:

transcription of DNA is stimulated

membrane bound receptors are activated

ion channels open

the Na+/K+ ATPase becomes active

Coursera Introduction to Physiology - Week 1 - Endocrine Concepts

1. Cells may communicate with one another by_____

A. transfering signal molecules to adjacent cells through gap junctions.

B. local-acting chemicals, called paracrines and autocrines

C. long-distance means, which rely on combinations of electrical and chemical signals.

D. A, B, and C

2. Which of the following statements is TRUE?

A. Autocrine and paracrine control use chemicals (ligands) to regulate cell activity.

B. Paracrine control is when a cell regulates its neighbor (local).

C. Target cells have receptors that recognize and bind the specific chemical (paracrine, autocrine or hormone).

D. A, B and C

3. Peptide hormones regulate their target cells by:

A. binding to cell surface receptors which activate intracellular signaling pathways

B. binding to DNA to change gene (DNA) expression.

C. binding to ion channels

D. B and C

One way to remember this is that peptide hormone are not ions, and there are not membrane permeable, so they have to do that on the cell surface receptors.

4. Which of the following statements correctly describes the mechanisms used by the tyrosine derivative hormones, epinephrine and thyroid hormone, to trigger their target cell’s response?

A. Thyroid hormone (TH) binds intracellular receptors to increase gene expression.

B. Thyroid hormone (TH) binds cell surface receptors triggering a rapid change in metabolism

C. Thyroid hormone and epinephrine binds intracellular receptors to increase gene expression

D. Thyroid hormone and epinephrine bind cell surface receptors triggering a rapid change in metabolism

Thyroid hormone is an amino acid derivative and is plasma membrane permeable. I have to remember this.

5. When steroid hormones bind to their receptors:

A. a second messenger pathway is activated.

B. G protein second messengers are inhibited.

C. gene transcription is activated

D. protein kinases are activated

6. Joanne presents to her physician with elevated plasma cortisol levels. She is administered dexamethasone, a drug used to suppress the secretion of ACTH from the pituitary gland. Her plasma cortisol levels fall to normal 60 minutes after the dexamethasone treatment. Joanne's condition is which of the following?

A. Primary pathology because the adrenal hormone, cortisol, was suppressed by the dexamethasone.

B. Secondary pathology because suppression of the pituitary hormone, ACTH, corrected the secretion of cortisol from the adrenal gland.

C. Tertiary pathology because the pituitary hormone ACTH was low in this patient.

The problem is that Joanne should not have high level of ACTH. The adrenal gland is functioning normally, but the Anterior Pituitary is not.

7. Which of the following statements is TRUE for steroid hormones?

A. They enter target cells by active transport.

B. They require carrier proteins for delivery to target tissues.

C. They are stored in secretory vesicles.

D. A, B and C

Steroid hormones are not plasma soluble and therefore requires carrier protein

8. The single most important factor that determines whether a specific gene in a given cell can be regulated by growth hormone is the presence in this cell of:

A. heat shock proteins

B. specific growth hormone receptors.

C. active transporters for growth hormone.

D. G proteins.

Coursera Introduction to Physiology - Week 1 - Transporter, Channel and Homeostasis

1. Cells may communicate with one another by:

A. transferring signal molecules to adjacent cells through gap junctions.

B. local chemicals, called paracrines and autocrines

C. chemicals that act at a distance.

D. A, B, and C

2. How does drinking one liter of water affect the fluid compartments of the body?

A. There are no changes in either the ECF or ICF.

B. The ECF increases by one liter with no change in the ICF.

C. The ECF will increase by 500 ml and the ICF by 500 ml.

D. The ECF will increase by 333 ml and the ICF increases by 666 ml.

This is because the osmolarity of fluid has to stay constant.

3. Complete the following true statement. Negative feedback loops ______ the initiating stimulus and positive feedback loops _____ the initiating stimulus.

A. increase; increase

B. remove; increase

C. increase; remove

D. remove; remove

4. In the following situation, identify the components of the reflex loop.

You have finished the marathon in just under three hours. You are tired, sweating profusely, and start to drink Gatorade. After several minutes you are still tired but no longer sweating or thirsty.

A. Stimulus (sweating); response (drinking)

B. Stimulus (drinking); response (sweating)

C. Stimulus (running); response (drinking)

I was confused with this one - since drinking is an activity that we choose to do, not an automatic response. But after all, given the choices, only this one make sense anyway.

5. Which of the following exhibits a circadian rhythm that coincides with sleep-wake cycles?

A. Cortisol secretion by adrenal glands

B. Acid secretion by stomach

C. Growth hormone secretion by pituitary

D. A and C

6. When plasma water is lost but electrolytes are retained, then:

A. osmolarity of the ECF falls

B. osmosis moves water from the ICF to the ECF

C. both the ICF and the ECF become more dilute

D. there is an increase in the volume of the ICF

Remember plasma is ECF

7. Which of the following solutions has the lowest concentration of water?

Solution   mM glucose   mM NaCl   mM CaCl2

A.         20           40       50

B.         20           50       80

C.         20           50       60

A. Solution A. It is 250 mOsM

B. Solution B. It is 360 mOsM

C. Solution C. It is 300 mOsM

The higher the concentration of solute, the lower the concentration of water.

8. Which of the following solutions is isotonic to a cell that is 300 mOsM?

Solution   mM glucose   mM NaCl   mM CaCl2

A.         20           40       50

B.         20           50       80

C.         20           50       60

Solution ______ is isotonic to a cell with an ICF of 300mOsM.

A. Solution A

B. Solution B

C. Solution C

The tonicity is computed using the number of particles of non-penetrating solute divided by the volume. We have 1 particle for glucose, 2 particles for NaCl and 3 particles for CaCl2

Therefore the tonicity are:
A) 20 + 2 x 40 + 3 x 50 = 250 mOsM
B) 20 + 2 x 50 + 3 x 80 = 360 mOsM
C) 20 + 2 x 50 + 3 x 40 = 300 mOsM

9. A neuronal cell with an ICF of 300mOsM will swell in which of the following solutions?

Solution   mM glucose   mM NaCl   mM CaCl2

A.         20           40       50

B.         20           50       80

C         20           50       60

A. Solution A which is 250 mOsM

B. Solution B which is 360 mOsM

C. Solution C which is 300 mOsM

Remember lower osmolarity, the higher the concentration of water. And therefore water moves from Solution A into the neuron because of the concentration gradient of water.

10. How does the addition of 10mM urea affect solution A?

Solution   mM glucose   mM NaCl   mM CaCl2

A.         20           40       50

B.         20           50       80

C         20           50       60

A. Increase the osmolarity by 10 mOsM

B. Increase the tonicity by 10 mOsM.

C. Increase the osmolarity and tonicity by 10 mOsM.

Urea can penetrate plasma membrane and therefore not included in the tonicity calculation.

11. Channels and symporters are alike because they facilitate diffusion of effective solutes across membranes as well as:

A. exhibit solute specificity

B. use ATP

C. exhibit saturation and solute specificity

D. exhibit saturation, solute specificity and use ATP

12. Channels are gated by which of the following?

A. ligands

B. voltage

C. tension (mechanical)

D. A and B

E. A, B and C

Denesting radicals

Problem:

Solution:

This is not a particular hard question, but I learn an interesting trick from it called the denesting of radicals, so I wanted to write this to remember.

The interesting thing to tackle is the $ \sqrt{5 - 2\sqrt{6}} $ and the $ \sqrt{8 - 2 \sqrt{15}} $ thing. They seems complicated, we would like to get rid of the nesting, so how?

Consider the general form and take a square of it and see what they look like:

$ (\sqrt{a} - \sqrt{b})^2 = a + 2\sqrt{ab} + b $

So if we wanted to make $ \sqrt{5 - 2\sqrt{6}}= \sqrt{a} - \sqrt{b} $, we need to find $ a + b = 5 $ and $ ab = 6 $, which is trivial in this case $ a = 3 $, $ b = 2 $. Obviously, we have to do big minus small to make sure it is positive.

Similarly, we have $ \sqrt{8 - 2 \sqrt{15}} = \sqrt{5} - \sqrt{3} $, the rest follows, in a very pleasing way, so I will do it here.

$ \begin{eqnarray*} \frac{x}{\sqrt{3}} + y &=& \sqrt{3} - 1 \\ x + \sqrt{3}y &=& 3 - \sqrt{3} \\ x &=& 3 - \sqrt{3} - \sqrt{3}y \end{eqnarray*} $
From the first equation, we can greatly simplify it as:

$ \begin{eqnarray*} x(\sqrt{3} - \sqrt{2}) + y(\sqrt{5} - \sqrt{3}) &=& \sqrt{3}(x + 1) + \sqrt{5}(y - 3) + 3(\sqrt{5} - \sqrt{2}) \\ \sqrt{3}x - \sqrt{2}x + \sqrt{5}y - \sqrt{3}y &=& \sqrt{3}x + \sqrt{3} + \sqrt{5}y - 3\sqrt{5} + 3\sqrt{5} - 3\sqrt{2} \\ \sqrt{3}x - \sqrt{2}x + \sqrt{5}y - \sqrt{3}y - \sqrt{3}x - \sqrt{5}y &=& \sqrt{3} - 3\sqrt{5} + 3\sqrt{5} - 3\sqrt{2} \\ \sqrt{3}x - \sqrt{3}x - \sqrt{2}x + \sqrt{5}y - \sqrt{5}y - \sqrt{3}y &=& \sqrt{3} - 3\sqrt{5} + 3\sqrt{5} - 3\sqrt{2} \\ - \sqrt{2}x - \sqrt{3}y &=& \sqrt{3} - 3\sqrt{2} \\ \sqrt{2}x + \sqrt{3}y &=& 3\sqrt{2} - \sqrt{3} \\ \end{eqnarray*} $
So at this point we simply substitute

$ \begin{eqnarray*} \sqrt{2}(3 - \sqrt{3} - \sqrt{3}y) + \sqrt{3}y &=& 3\sqrt{2} - \sqrt{3} \\ 3\sqrt{2} - \sqrt{2}\sqrt{3} - \sqrt{2}\sqrt{3}y + \sqrt{3}y &=& 3\sqrt{2} - \sqrt{3} \\ -\sqrt{2}\sqrt{3}y + \sqrt{3}y &=& 3\sqrt{2} - \sqrt{3} - 3\sqrt{2} + \sqrt{2}\sqrt{3} \\ (-\sqrt{2}\sqrt{3}+\sqrt{3})y &=& 3\sqrt{2} - \sqrt{3} - 3\sqrt{2} + \sqrt{2}\sqrt{3} \\ (-\sqrt{2}\sqrt{3}+\sqrt{3})y &=& - \sqrt{3} + \sqrt{2}\sqrt{3} \\ y &=& -1 \end{eqnarray*} $
$ \begin{eqnarray*} x &=& 3 - \sqrt{3} - \sqrt{3}y \\ x &=& 3 - \sqrt{3} + \sqrt{3} \\ x &=& 3 \end{eqnarray*} $

Does it looks very complicated, yes, it is intended to make it look like so :p

Moon area problem

Problem:

Solution:

I am an engineer, therefore I am thinking about solving this using integration. But the area defined is hard to compute using integration because the curves defining it are not functions. (For example, at the far right end, the circle has both its upper point and lower point), so I figured something else.

 The yellow area is what we wanted, note that it is super easy to calculate the red area, as well as the sum of all colored areas, which leave us the question, how to we compute the green area? Because if we can compute the green area, the problem is pretty much solved.

The red area is simply the difference between a square of side 0.5 and a quarter circle with radius 0.5), so it is $ 0.5^2 - \frac{\pi 0.5^2}{4} \approx 0.053650459 $

The sum of all colored area is simply the same shape with side doubled, so the area is four times the red area and it is approximately $ 0.053650459 \times 4 \approx 0.214601837 $

Next we focus on the green area, zooming in, we see that is a sum of two areas, the dark green and the light green one, it is now obvious that the left one can be solved by integration, it is not so obvious that the right one can be computed relatively easily with the left hand side result as we shall see.

You probably see in the diagram that the x coordinate of the intersection point is approximately 0.29, why is that?

Let's solve this:

The equation of the big circle is $ x^2 + (y - 1)^2 = 1 \implies x^2 + y^2 - 2y = 0 $.
The equation of the small circle is $ (x - 0.5)^2 + (y - 0.5)^2 = (0.5)^2 \implies x^2 + y^2 - x - y + 0.25 = 0 $

Subtracting these two equations give $ x - y - 0.25 = 0 \implies y = x - 0.25 $.

Putting this back into the first equation gives $ x^2 + (x - 0.25 - 1)^2 = 1 $, solving we get $ x = 2x^2 - 2.5x + 0.5625 = 0 $ and therefore $ x = \frac{2.5 \pm \sqrt{1.75}}{4} $, we take the smaller value $ \frac{2.5 - \sqrt{1.75}}{4} $ as this is the leftmost intersection point.

Next, we compute we find an explicit formula for the lower big circle. We already have the implicit form: $ x^2 + (y - 1)^2 = 1 $, making $ y $ the subject gives $ y = 1 \pm \sqrt{1 - x^2} $, as this is the lower half of the circle so we take the negative sign $ y = 1 - \sqrt{1 - x^2} $

Now we do the integration, the form is simply asking for trigonometric subsitution, so we are doing it.

Let $ x = \sin u $, $ dx = \cos u du $

$ \int{1 - \sqrt{1 - x^2}dx} $
$ \int{(1 - \sqrt{1 - \sin^2 u})\cos u du} $
$ \int{(1 - \sqrt{\cos^2 u})\cos u du} $
$ \int{(1 - \cos u)\cos u du} $
$ \int{(\cos u - \cos^2 u) du} $
$ \int{(\cos u - \frac{1 + \cos 2u}{2}) du} $
$ \sin u - \frac{1}{2}(u + \frac{1}{2}\sin 2u) $
$ \sin u - \frac{1}{2}(u + \sin u \cos u) + C $
$ x - \frac{1}{2}(\arcsin x + x \sqrt{1 - x^2}) + C $

This formula gives us the dark green area (note that we can just set $ C = 0 $ as the formula gives 0 when $ x = 0 $)

If we substitute the number, the dark green area is approximately $ 0.004304482 $

If we observe carefully, the light green area is actually a similar figure. If we double the image so that the small circle has radius 1, the shape of the area is exactly the same, so we can use exactly the same formula there.

The base has length $ 2 \times (0.5 - 0.29) $ long in the doubled area, we plug in the formula, and then scale it back down (so that area is divided by 4), we get the value $ 0.002980577 $

Last but not least, given all the areas, we can now compute the moon area to be $ 0.14638126 $.

Using this simple C# Monte Carlos simulation program, I verified the answer above should be correct.

namespace Moon
{
    using System;

    class Program
    {
        static void Main(string[] args)
        {
            Random random = new Random(0);
            int numTrials = 10000000;
            int hitTrials = 0;
            for (int i = 0; i < numTrials; i++)
            {
                double x = random.NextDouble();
                double y = random.NextDouble();
                bool outsideQuarter = (x * x + y * y) > 1;
                bool insideCircle = (x - 0.5) * (x - 0.5) + (y - 0.5) * (y - 0.5) < 0.25;
                bool insideMoon = outsideQuarter && insideCircle;
                if (insideMoon)
                {
                    hitTrials++;
                }
            }
            Console.WriteLine((hitTrials + 0.0) / numTrials);
        }
    }
}

One last problem remain though, is there a simpler solution?

UTM Ideals Varieties and Algorithm - Chapter 2 Section 2 Exercise 7

Problem:

Solution:

It took me a good while to solve this problem, but looking in retrospect, this problem is easy. It is just that the notation tripped me up.

(a)

First, note that $ \alpha \in \mathbf{Z}_{\ge 0}^{n} $, so $ \alpha = 0 $ means it is an n-tuple of all 0, which means all the powers are 0, which means the monomial is actually 1, not 0.

With that in mind, the solution for this is not hard, we do infinity descent here as follow. Suppose the contrary, we have :

$ 0 > \beta $ for some $ \beta $
$ \beta = 0 + \beta  > \beta + \beta =2\beta $
$ 2\beta = 0 + 2\beta > \beta + 2\beta = 3\beta $

and so on.

Now we have a sequence of $ 0, \beta, 2\beta, 3\beta, \cdots $ and this is an infinitely decreasing sequence with no minimum, contradicting the well ordering property required for monomial order.

(b)

Now we know 1 as a term is the minimum monomial for all order, in particular, we know

$ 1 \le x^{\beta - \alpha} $

Multiplying $ x^{\alpha} $ on both side we get the inequality we wanted

$ x^{\alpha} \le x^{\beta} $.

The converse is not true, in particular, we know in lex order

$ x < y $.

But obviously neither divide each other.

(c)

We do a similar infinite descent for this one, support the contrary, we have

$ \alpha + \beta < \alpha $

We reach the same conclusion as above, to be more concrete, we can write

$ \alpha + \beta +k\beta < \alpha + k\beta $.

So we have the sequence $ \alpha, \alpha + \beta, \alpha + 2\beta, \cdots $. This is an infinitely decreasing sequence with no minimum, so again it contradicts the well ordering property.

The Art of Computer Programming - Section 1.2.3, First Set, Exercise 16

Problem:

Solution:

The trick is to differentiate the geometric series on both side


$ \begin{eqnarray*} \sum\limits_{j = 0}^{n}x^j &=& \frac{x^{n+1} - 1}{x - 1} \\ \frac{d}{dx}(\sum\limits_{j = 0}^{n}x^j) &=& \frac{d}{dx}(\frac{x^{n+1} - 1}{x - 1}) \\ \sum\limits_{j = 0}^{n}\frac{d}{dx}(x^j) &=& \frac{d}{dx}(\frac{x^{n+1} - 1}{x - 1}) \\ \sum\limits_{j = 0}^{n}jx^{j - 1} &=& \frac{d}{dx}(\frac{x^{n+1} - 1}{x - 1}) \\ \sum\limits_{j = 0}^{n}jx^j &=& x\frac{d}{dx}(\frac{x^{n+1} - 1}{x - 1}) \\ &=& x\frac{(x-1)(x^{n+1} - 1)' - (x^{n+1} - 1)(x-1)'}{(x - 1)^2} \\ &=& x\frac{(x-1)(n+1)x^n - (x^{n+1} - 1)}{(x - 1)^2} \\ &=& x\frac{(n+1)x^{n+1} - (n+1)x^n - x^{n+1} + 1}{(x - 1)^2} \\ &=& x\frac{nx^{n+1} - (n+1)x^n + 1}{(x - 1)^2} \\ &=& \frac{nx^{n+2} - (n+1)x^{n+1} + x}{(x - 1)^2} \\ \end{eqnarray*} $

A primer for mathematics competitions - Section 1.2 - Appetizer Problem

Problem:

Solution:

Here I present my solution. The book's solution is MUCH simpler but that is not mine.

We know $ BX : XC = 2:3 $, so let $ \vec{BX} = 2\vec{p} $. $ \vec{XC} = 3\vec{p} $.
Similarly, $ \vec{CY} = \vec{q} $, $ \vec{YA} = 2\vec{q} $.

Let $ \vec{AB} = \vec{r} $, our goal is to compute the length ratios.

$ \vec{AX} = \vec{AB} + \vec{BX} = \vec{r} + \vec{2p} $.
$ \vec{AX} = \vec{AC} + \vec{CX} = (-3\vec{q}) - \vec{3p} $.

Therefore: $ \vec{AX} = \frac{1}{5}(3\vec{r} - 6\vec{q}) $ (Just eliminate $ \vec{p} $ from the equations above)

$ \vec{BY} = \vec{BA} + \vec{AY} = -\vec{r} - 2\vec{q} $

Observe that we have two ways to get to $ O $, either starting from $ A $ or $ B $.

Let $ \vec{AO} = \alpha \vec{AX} $
Let $ \vec{BO} = \beta \vec{BY} $

Now $ \alpha ( \frac{1}{5}(3\vec{r} - 6\vec{q})) = \alpha \vec{AX} = \vec{AO} = \vec{AB} + \vec{BO} = \vec{r} + \beta \vec{BY} = \vec{r} + \beta(-\vec{r} - 2\vec{q}) $

Now the amazing thing happens, we can solve $ \alpha $ and $ \beta $ at the same time by equating coefficients.

$ \alpha ( \frac{1}{5}(3\vec{r} - 6\vec{q})) = \vec{r} + \beta(-\vec{r} - 2\vec{q}) $

$ \frac{3}{5}\alpha = 1 - \beta $ (matching coefficients of $ \vec{r} $)
$ -\frac{6}{5}\alpha = -2\beta $ (matching coefficients of $ \vec{q} $)

Solving, get $ \alpha = \frac{5}{6} $, $ \beta = \frac{1}{2} $.

So $ AO : OX = 5 : 1 $, $ BO : OY = 1 : 1 $.

Next, we tackle the $ CO:OZ $ and $ AZ : ZB $. To do that, we compute $ CO $ in two ways.

Let $ \vec{CO} = \gamma \vec{CZ} $
Let $ \vec{AZ} = \delta \vec{AB} $

$ \vec{CO} = \vec{CB} + \vec{BO} = \vec{CA} + \vec{AB} +  \frac{1}{2}\vec{BY} = 3\vec{q} + \vec{r} + \frac{1}{2}(-\vec{r} - 2\vec{q}) = \frac{1}{2}(\vec{r} + 4\vec{q}) $

$ \vec{CZ} = \vec{CA} + \vec{AZ} = \vec{3q} + \delta \vec{AB} = \vec{3q} + \delta\vec{r} $.

Now $ \frac{1}{2}(\vec{r} + 4\vec{q}) \vec{CO} = \gamma \vec{CZ} = \gamma(\vec{3q} + \delta\vec{r}) $

Now we equate coefficients again and get

$ \frac{1}{2} = \gamma \delta $ (matching coefficients of $ \vec{r} $)
$ 2 = 3\gamma $

Solving, get $ \gamma = \frac{2}{3} $, $ \delta = \frac{3}{4} $.

So $ CG : GZ = 2 : 1 $, $ AZ:ZB = 1 : 3 $.

Now at this point, we have all the length ratios we wanted. For triangles with opposite angle, we know triangle area is $ \frac{1}{2}ab\sin\theta $, so the length ratio give us triangle area ratios.

Since we do not need to vectors anymore, abusing the notation, we reuse $ P Q R S T U $ to mean the triangle areas of $ \triangle AOZ, \triangle AOY, \triangle ZOB, \triangle YOC, \triangle BOX, \triangle XOC $.

The length ratios give us these equations:

$ 2P = 5U $
$ R = 2S $
$ 5T = Q $

We wanted $ R + T $, but we do not know $ Q $, so even more is required. Here is another observation, $ \triangle ABX : \triangle ACX = 2:3 $ because they share the same height but with different base, that gives $ 3(P + R + T) = 2(Q + S + U) $, at this point, we can solve $ Q = \frac{5.5U + 4S}{1.4} $, and therefore $ R + T = 2a + \frac{16.5b + 4a}{7} $.

Even then, it is not enough, because we have no matching answer, now we pull in one more equation with the observation that $ \triangle CAE : \triangle CBE = 3:1 $ using the similar argument, now we get 5 equations:

$ 2P = 5U $
$ R = 2S $
$ 5T = Q $
$ 3(P + R + T) = 2(Q + S + U) $
$ P + Q + S = 3(R + T + U) $,

We know these equations will not give an exact answer because it is simply up to scaling. We arbitrarily set $ U = 1 $ and solve these equations (with a solver, coz I am lazy), we finally get our answers.

P = 2.500
Q = 4.722
R = 0.556
S = 0.278
T = 0.944
U = 1.000

So R + T = 1.5 and that is $ \frac{9}{2}\frac{1}{3} = \frac{9b}{2} $

So finally, that's our answer! Phew.

UTM Ideals Varieties and Algorithm - Chapter 2 Section 2 Exercise 6

Problem:

Solution:

It is simply reversing the variable order.

Suppose a set of polynomial is invlex ordered with respect to the variable order $ x > y > z $, then it is lex ordered with respect to the variable order $ z > y > x $, this is obvious to see from the definition.

A primer for mathematics competitions - Section 1.1 - Appetizer Problem 3

Problem:

Solution:

We know the method for computing the radius for the inscribed circle. Now let's think about the radius of the circumscribed circle.

The key observation is that it is a right angled triangle inside a circle, so the hypotenuse must be the diameter, and therefore $ R = \frac{c}{2} $, in our previous case, that would be $ \frac{5}{2} $.

To avoid the algebra, we can simply test the options and see which one gives $ 1 : 2.5 $. That gives option (A) right away.

Knowing the answer is (A), working backwards, we know the radius of the inscribed circle is $ \frac{ab}{a + b + c} $.

This is a particularly good looking formula. Let's see why.

Using exactly the same computation we had in the last problem, we have

$ \frac{d}{a} = \frac{1 - \frac{a}{c}}{\frac{b}{c}} = \frac{c - a}{b} $.

The equation of the angle bisector is

$ \frac{x}{a} + \frac{y}{\frac{a(c-a)}{b}} = 1 $.

Solving for $ x $ by subsituting $ y = x $, we get

$ x = \frac{a}{1 + \frac{b}{c-a}} = \frac{a (c - a)}{b + c - a} $ and that is our representation for the radius of the inscribed circle.

I claim that the two representations are equal, to see that, we write

$ \begin{eqnarray*} \frac{a (c - a)}{b + c - a} &=& \frac{ab}{a+b+c} \\ a (c - a)(a + b + c) &=& (ab)(b + c - a) \\ a^2c + abc + ac^2 - a^3 - a^2b - a^2c &=& ab^2 + abc - a^2b \\ abc + ac^2 - a^3 - a^2b &=& ab^2 + abc - a^2b \\ ac^2 - a^3 &=& ab^2 \\ ac^2 - a^3 &=& a(c^2 - a^2) \\ ac^2 - a^3 &=& ac^2 - a^3 \end{eqnarray*} $

Reading backwards, now we have shown the both representations are equal (of course, the given one look much better)

A primer for mathematics competitions - Section 1.1 - Appetizer Problem 2

Problem:

Solution:

There must be a lot of different ways to approach this problem, but personally, I like to address geometric problem analytically, or even better, algebraically.

First, we recall the fact that an inscribed circle's center is at the intersections of the angle bisectors. The equation of the angle bisector for the right angle is particularly easy, it is simply $ y = x $, now if we found another angle bisector's equation, then we are done.

Suppose we draw the angle bisector of the angle between the hypotenuse and the base, we get a diagram like this.

I want to find the y-intercept value $ d $ of that angle bisector, because then I can use intercept form for straight-line to find the equation of it. Now we know that $ \frac{d}{3} = \tan\frac{\alpha}{2} $, now we can use this awesome formula I found online.

$ \tan{\frac{\alpha}{2}} = \frac{1-\cos\alpha}{\sin\alpha} $

Now we can easily calculate $ d = 3\tan{\frac{\alpha}{2}} = 3\frac{1-\cos\alpha}{\sin\alpha} = 3\frac{1 - \frac{3}{5}}{\frac{4}{5}} = \frac{3}{2} $.

Therefore, the angle bisector's equation is $ \frac{x}{3} + \frac{y}{\frac{3}{2}} = 1 $, in intercept form.

Solving the intersection point of this with $ y = x $ gives $ x = y = 1 $, that is the center of our inscribed circle, and therefore the radius is also 1.

So the answer is (A) - A for appetizer?

A primer for mathematics competitions - Section 1.1 - Appetizer Problem 1

Problem:

Solution:

Letting the center of the circle $ O $, the square to have side length $ 2s $ and the circle have radius $ r $.

By Pythagoras theorem, we can get this relation. (Sorry Pythagoras, I just keep forgetting how to spell your name ... )

$ s^2 + (2s - r)^2 = r^2 $

This can easily simplify to $ 5s^2 - 4sr = 0 $, so we get $ r = \frac{5s}{4} $.

Therefore the area ratio is $ \frac{\pi r^2}{(2s)^2} = \frac{\pi (5s)^2}{4^2(2s)^2} = \frac{25\pi }{64} $.

The answer is (A).

UTM Ideals Varieties and Algorithm - Chapter 2 Section 2 Exercise 5

Problem:

Solution:

All we needed to do for this problem is to verify the three rules.

(i) > is a total (or linear order) on $ \mathbf{Z}^n_{\ge 0} $

This is simple to verify according to the definition. As long as two monomials are not the same, then either one is strictly larger than the other.

(ii) If $ \alpha > \beta $ and $ \gamma \in \mathbf{Z}^n_{\ge 0} $, then $ \alpha + \gamma > \beta + \gamma $.

This is also simple to verify. if $ \alpha $ has a total degree larger than $ \beta $, then so is $ \alpha + \gamma $ and $ \beta + \gamma $. Otherwise if the rightmost element of $ \alpha - \beta $ is negative, then so is $ \alpha + \gamma $ and $ \beta + \gamma $ as well.

(iii) > is a well ordering

For any set of $ n $ tuple, their total order is a set of non-negative integer and therefore there exist a smallest total degree, consider that subset of $ n $ tuples with smallest total degree.

For any set of $ n $ tuple with the same total order, their last element is an integer, and therefore exists a smallest first element, consider that subset of $ n $ tuples with smallest total degree and smallest last element. (*)

Repeat the above until we find the one with every element smallest. Now we have found a smallest element.

Suppose we have two elements $ \alpha $ and $ \beta $ with same total degree to compare with and $ \alpha $ has a smallest last element, then $ \alpha - \beta $ will have a negative rightmost non-zero element.

UTM Ideals Varieties and Algorithm - Chapter 2 Section 2 Exercise 4

Problem:

Solution:

All we needed to do for this problem is to verify the three rules.

(i) > is a total (or linear order) on $ \mathbf{Z}^n_{\ge 0} $

This is simple to verify according to the definition. As long as two monomials are not the same, then either one is strictly larger than the other.

(ii) If $ \alpha > \beta $ and $ \gamma \in \mathbf{Z}^n_{\ge 0} $, then $ \alpha + \gamma > \beta + \gamma $.

This is also simple to verify. if $ \alpha $ has a total degree larger than $ \beta $, then so is $ \alpha + \gamma $ and $ \beta + \gamma $. Otherwise if $ \alpha $ is lexicographically larger than $ \beta $, then so is $ \alpha + \gamma $ and $ \beta + \gamma $ as well.

(iii) > is a well ordering

For any set of $ n $ tuple, their total order is a set of non-negative integer and therefore there exist a smallest total degree, consider that subset of $ n $ tuples with smallest total degree.

For any set of $ n $ tuple with the same total order, their first element is an integer, and therefore exists a smallest first element, consider that subset of $ n $ tuples with smallest total degree and smallest first element.

Repeat the above until we find the one with every element smallest. Now we have found a smallest element.

Convex Optimization Exercise 2.1

Problem:

Solution:

The case for $ k = 1 $ is trivial. The case for $ k = 2 $ is given as definition. Using induction, we can assume $ \theta_1 x_1 + \cdots + \theta_{k-1} x_{k-1} \in C $ work for any set of $ \theta $ that sums to 1.

Now consider

$ \begin{eqnarray*} & & \theta_1 x_1 + \cdots + \theta_k x_k \\ &=& \theta_1 x_1 + \cdots + \theta_{k-1} x_{k-1} + \theta_k x_k \\ &=& \frac{1 - \theta_k}{1 - \theta_k}(\theta_1 x_1 + \cdots + \theta_{k-1} x_{k-1}) + \theta_k x_k \\ &=& (1 - \theta_k)(\frac{\theta_1}{1 - \theta_k} x_1 + \cdots + \frac{\theta_{k-1}}{1 - \theta_k} x_{k-1}) + \theta_k x_k \end{eqnarray*} $

Now we know the sum inside the bracket is in $ C $ by the induction hypothesis, and therefore the point we wanted to prove is also in $ C $ because of the definition.

UTM Ideals Varieties and Algorithm - Chapter 2 Section 2 Exercise 3

Problem:

Solution:

Here is the Exercise 1 statement.

Okay, I know this is stupid, this is just an exercise!

Part (a)
lex order: $ -z^2 + z + 3y + x^3 + x^2 + 2x $
$ LM(f) = z^2 $
$ LT(f) = -z^2 $
$ multideg(f) = (2, 0, 0) $
(2, 0, 0)
(1, 0, 0)
(0, 1, 0)
(0, 0, 3)
(0, 0, 2)
(0, 0, 1)

grlex order: $ x^3 - z^2  + x^2 + z + 3y + 2x $
$ LM(f) = x^3 $
$ LT(f) = x^3 $
$ multideg(f) = (0, 0, 3) $
(0, 0, 3)
(2, 0, 0)
(0, 0, 2)
(1, 0, 0)
(0, 1, 0)
(0, 0, 1)

grevlex order: $ x^3 + z^2 - x^2 + z + 3y + 2x $
$ LM(f) = x^3 $
$ LT(f) = x^3 $
$ multideg(f) = (0, 0, 3) $
(0, 0, 3)
(2, 0, 0)
(0, 0, 2)
(1, 0, 0)
(0, 1, 0)
(0, 0, 1)

Part (b)
lex order: $ -3x^5yz^4  + xyz^3 + 2x^2y^8 - xy^4 $
$ LM(f) = x^5yz^4 $
$ LT(f) = - 3x^5yz^4 $
$ multideg(f) = (4, 1, 5) $
(4, 1, 5)
(3, 1, 1)
(0, 8, 2)
(0, 4, 1)

grlex order: $ -3x^5yz^4 + 2x^2y^8 + xyz^3 - xy^4 $
$ LM(f) = x^5yz^4 $
$ LT(f) = - 3x^5yz^4 $
$ multideg(f) = (4, 1, 5) $
(4, 1, 5)
(0, 8, 2)
(3, 1, 1)
(0, 4, 1)

grevlex order: $ 2x^2y^8 - 3x^5yz^4 + xyz^3 - xy^4 $
$ LM(f) = x^2y^8 $
$ LT(f) =  2x^2y^8 $
$ multideg(f) = (0, 8, 2) $
(0, 8, 2)
(4, 1, 5)
(3, 1, 1)
(0, 4, 1)

UTM Ideals Varieties and Algorithm - Chapter 2 Section 2 Exercise 2

Problem:

Solution:

Part (a) grlex
Part (b) grevlex
Part (c) lex

UTM Ideals Varieties and Algorithm - Chapter 2 Section 2 Exercise 1

Problem:

Solution:

It is a really simple sorting exercise, so let's do some warmup.

Part (a)
lex order: $ x^3 + x^2 + 2x + 3y - z^2 + z $
$ LM(f) = x^3 $
$ LT(f) = x^3 $
$ multideg(f) = (3, 0, 0) $
(3, 0, 0)
(2, 0, 0)
(1, 0, 0)
(0, 1, 0)
(0, 0, 2)
(0, 0, 1)

grlex order: $ x^3 + x^2 - z^2 + 2x + 3y + z $
$ LM(f) = x^3 $
$ LT(f) = x^3 $
$ multideg(f) = (3, 0, 0) $
(3, 0, 0)
(2, 0, 0)
(0, 0, 2)
(1, 0, 0)
(0, 1, 0)
(0, 0, 1)

grevlex order: $ x^3 + x^2 - z^2 + 2x + 3y + z $
$ LM(f) = x^3 $
$ LT(f) = x^3 $
$ multideg(f) = (3, 0, 0) $
(3, 0, 0)
(2, 0, 0)
(0, 0, 2)
(1, 0, 0)
(0, 1, 0)
(0, 0, 1)

Part (b)
lex order: $ -3x^5yz^4 + 2x^2y^8  - xy^4 + xyz^3 $
$ LM(f) = x^5yz^4 $
$ LT(f) = - 3x^5yz^4 $
$ multideg(f) = (5, 1, 4) $
(5, 1, 4)
(2, 8, 0)
(1, 4, 0)
(1, 1, 3)

grlex order: $ -3x^5yz^4 + 2x^2y^8  - xy^4 + xyz^3 $
$ LM(f) = x^5yz^4 $
$ LT(f) = - 3x^5yz^4 $
$ multideg(f) = (5, 1, 4) $
(5, 1, 4)
(2, 8, 0)
(1, 4, 0)
(1, 1, 3)

grevlex order: $ 2x^2y^8 - 3x^5yz^4 - xy^4 + xyz^3 $
$ LM(f) = x^2y^8 $
$ LT(f) =  2x^2y^8 $
$ multideg(f) = (2, 8, 0) $
(2, 8, 0)
(5, 1 ,4)
(1, 4, 0)
(1, 1, 3)

Differential Geometry of Curves and Surfaces - Chapter 1 Section 3 Exercise 3

Problem:

Note the errata to this problem here. In particular, B should be on the line with OC and that's the half line r.

Solution:

Note that $ \angle OCA $ is a right angle.

$ \frac{CA}{2a} = \sin \theta $
$ \frac{BA}{2a} = \tan \theta $
$ CA^2 + CB^2 = BA^2 $

$ (2a \sin \theta)^2 + CB^2 = (2a \tan \theta)^2 $
$ OP^2 = CB^2 = 4a^2(\tan^2 \theta - \sin^2 \theta) $

With some trigonometry, we get

$ \sec^2 \theta = 1 + \tan^2 \theta = 1 + t^2 $
$ \cos^2 \theta = \frac{1}{\sec^2 \theta} = \frac{1}{1 + t^2} $
$ \sin^2 \theta = 1 - \cos^2 \theta = 1 - \frac{1}{1 + t^2} = \frac{t^2}{1 + t^2} $
$ \tan^2 \theta - \sin^2 \theta = t^2 - \frac{t^2}{1 + t^2} = \frac{t^4 + t^2 - t^2}{1 + t^2} = \frac{t^4}{1 + t^2} $

So we get $ OP = \frac{2at^2}{\sqrt{1 + t^2}} $

$ x = OP \cos \theta = \frac{2at^2}{1 + t^2} $
$ y = OP \sin \theta = \frac{2at^3}{1 + t^2} $

This time around I solved the problem with a good diagram and geometrical insight without using MATLAB.

Part (b) is trivial, when $ t \to \pm \infty $, $ x \to 2a $, $ y \to 0 $,

$ \alpha' = 2a\frac{1}{(1+t^2)^2}((1 + t^2)2t - t^2(2t), (1 + t^2)3t^2 - t^3(2t)) $

So $ \alpha'(t) = (0, 2a) $ as $ t \to \pm \infty $

At this point I am still confused, look like $ \alpha'(t) $ should be $ (0, 2a) $ and not $ (2a, 0) $?

Problems in Number Theory

Problem:

Solution:

The key step in this problem is to let $ n = A2^p3^q5^r $, it can be easily seen that $ A = 1 $ for minimal value in the set.

The fact that these roots are natural number give rise to these equations:

$ p - 1 = 0 \mod 2 $
$ p = 0 \mod 3 $
$ p = 0 \mod 5 $

$ q = 0 \mod 2 $
$ q - 1 = 0 \mod 3 $
$ q = 0 \mod 5 $

$ r = 0 \mod 2 $
$ r = 0 \mod 3 $
$ r - 1 = 0 \mod 5 $

By Chinese remainder theorem, we get $ p = 15 $, $ q = 10 $, $ r = 6 $, so the answer is

$ 2^15 \times 3^10 \times 5^6 = 30,233,088,000,000 $

UTM Ideals Varieties and Algorithm - Chapter 2 Section 1 Exercise 5

Problem:

Solution:

For part (a), the number of monomials is easy to count by listing them in a pyramid like this

$
\begin{array}{cccc}
   x^0 &            &        &        \\
   x^1 & y^1        &        &        \\
   x^2 & x^1y^1     & y^2    &        \\
\cdots & \cdots     & \cdots &  \\
   x^m & x^{m-1}y^1 & \cdots & y^m
\end{array}
$

Now counting them is trivial, it is just $ 1 + 2 + \cdots + (m + 1) = \frac{(m+1)(m+2)}{2} $

For part (b), I read part (c) as a hint. It doesn't quite mention what does it mean by "monomial" and "linear dependent".

I figured it actually means regarding polynomial as vectors. Notice when we add two polynomials, we need to match the degree when we add terms together, so a polynomial is really a vector (can be think of as tuple of numbers).

Now, let imagine if we expand $ [f(t)]^a[g(t)]^b $, the lowest degree term is constant, and the highest degree term is $ t^{na}t^{nb} \le t^{mn} $, and the expansion could have terms of any power of $ t $ in between. We can then think of them as vector space of dimension $ mn + 1 $

If we think of the collection of all polynomials of form $ [f(t)]^a[g(t)]^b $, by part (a), there are $ \frac{(m+1)(m + 2)}{2} $ of them, and all of them are vectors of dimension $ mn + 1 $, so if $ \frac{(m+1)(m + 2)}{2} > mn + 1 $, then by definition these vectors must be linear dependent.

As for part (c), we know those 'vectors' are linear dependent. We can find ourselves a formula $ \sum a_i p_i = 0 $, because these $ p_i $ are just $ x^a y^b $, so the overall formula is a polynomial in $ k[x, y] $.

Suppose a point is on the parametric curve, we know for sure that it is on the polynomial we found. On the other hand, for a point on the polynomial, we do NOT really know if it is on the parametric curve or not, that's why the problem is carefully crafted and say that the parametric curve is contained in the variety, not that the parametric curve IS the variety.

Part (d) is basically the same idea as part (b) and (c) except we go up one dimension. We consider the 'monomial' $ [f(t, u)]^a[g(t, u)]^b[h(t, u)]^c $.

To count the number of these 'monomials', we need to be more imaginative. Consider a pile of balls arranged in a tetrahedral shape like this.

The red ball represents the 'monomial' $ [f(t,u)]^0[g(t, u)]^0[h(t, u)]^0 $, the blue ball represents $ [f(t,u)]^1[g(t, u)]^0[h(t, u)]^0 $ and so on. The total number of 'monomials' is known as the tetrahedral numbers and there is $ \frac{m(m+1)(m+2)}{6} $ of them.

The total number of terms in such expression, however, is going to be bounded by the degree of $ t $ and $ u $ just like what we did in part (b). The maximum degree in $ t $ and $ u $ is both mn. So there can be at most $ (mn + 1)^2 $ terms.

Therefore we can still pick $ m $ such that $ \frac{m(m+1)(m+2)}{6} > (mn+1)^2 $ and therefore we can still argue for the vectors being linearly dependent.

Once we have that linear dependency, we can have the  $ \sum a_i p_i = 0 $ expression again, and once again that will be our $ F $ for the surface case!

UTM Ideals Varieties and Algorithm - Chapter 2 Section 1 Exercise 4

Problem:

Solution:

For part (a), in order to show a set is an ideal, we check the two conditions for ideals.

Condition 1: If $ a \in I $, then $ h a \in I $ for all $ h \in R $.

This is true for I because if $ a \in I $, then $ a = x_{t_1}f_1 +  \cdots + x_{t_m}f_m $,
so $ ha = h(x_{t_1}f_1 +  \cdots + x_{t_m}f_m) = x_{t_1}(hf_1) +  \cdots + x_{t_m}(hf_m) \in I $.

Condition 2: If $ a \in I $ and $ b \in I $, then $ a + b \in I $.

This is also true because

$ a \in I $, then $ a = x_{t_1}f_1 +  \cdots + x_{t_m}f_m $,
$ b \in I $, then $ b = x_{u_1}g_1 +  \cdots + x_{u_m}g_m $,

The sum then must also be the same form and therefore $ a + b \in I $.

For part (b), if $ I $ has a finite generating set, then each element is a polynomial and therefore by definition above, a finite linear combination of monomials.

Therefore the number of variables involved in that finite generating set must be finite, but the ideal has infinite number of variables. So there cannot be a finite generating set.

UTM Ideals Varieties and Algorithm - Chapter 2 Section 1 Exercise 3

Problem:

Solution:

For part (a), note that according to the errata, the last equation should be $ x_3 = -t + 6 $.

First note that all the equations are linear and there is one parameter, it is a line. We should expect two linear equations defining two planes.

From the first equation, it is obvious that $ t = x_1 + 5 $, so we get from the second equation $ x_2 = 2t + 1 = 2 (x_1 + 5) + 1 = 2x_1 + 11 $, and from the third equation $ x_3 = -t + 6 = -(x_1 + 5) + 6 = 1 - x_1 $, so the solution is:

$ x_2 = 2x_1 + 11 $
$ x_3 = 1 - x_1 $

Part (b) is more complicated, it is a two dimensional 'plane' in a 4 dimensional space. Adhoc methods like the previous problem does not work great, so we will try something different. We model the problem using this matrix.

$ \begin{array}{ccccccc}t & u & x_1 & x_2 & x_3 & x_4 & t\\2 & -5 & -1 & 0 & 0 & 0 & 0\\1 & 2 & 0 & -1 & 0 & 0 & 0\\-1 & 1 & 0 & 0 & -1 & 0 & 0\\1 & 3 & 0 & 0 & 0 & -1 & 0\end{array} $

Next, we find the reduced row echelon form using MATLAB (using the function rref), and we get this.

$ \begin{array}{ccccccc}t & u & x_1 & x_2 & x_3 & x_4 & t\\1 & 0 & 0 & 0 & 0.75 & -0.25 & 0\\0 & 1 & 0 & 0 & -0.25 & -0.25 & 0\\0 & 0 & 1 & 0 & 2.75 & 0.75 & 0\\0 & 0 & 0 & 1 & 0.25 & -0.75 & 0\end{array} $

We claim that the last two rows is our solution. To see that, any point that satisfied the parametrization must satisfy all four equations, and therefore it satisfy the last two. For any point satisfy the last two equations, we can always find $ t $ and $ u $ by equation 1 and 2, so we have proved the answer is

$ x_1 + 2.75x_3 + 0.75x_4 = 0 $

$ x_2 + 0.25x_3 - 0.75x_4 = 0 $

Part (c) is pretty easy, it is simple to inspect the answer is

$ x^4 = y $

$ x^7 = z $

Differential Geometry of Curves and Surfaces - Chapter 1 Section 3 Exercise 2

Problem:

Solution:

We will skip part (a) because it is basically the same as this previous exercise. The solution is $ (t - \sin t, 1 - \cos t) $

For part (b), we compute the arc length as

$ \begin{eqnarray*} & & \int\limits_{0}^{2\pi}{\left|\alpha'(t)\right|dt} \\ &=& \int\limits_{0}^{2\pi}{\sqrt{\alpha'(t) \cdot \alpha'(t)}dt} \\ &=& \int\limits_{0}^{2\pi}{\sqrt{(1-\cos t)^2 + \sin^2 t}dt} \\ &=& \int\limits_{0}^{2\pi}{\sqrt{1 - 2\cos t + \cos^2 t + \sin^2 t}dt} \\ &=& \int\limits_{0}^{2\pi}{\sqrt{2 - 2\cos t}dt} \\ \end{eqnarray*} $

The rest is really just an integration problem, let $ x = \cos t $, so

$ \begin{eqnarray*} dx &=& -\sin t dt \\ &=& -\sqrt{1 - \cos^2 t} dt \\ &=& -\sqrt{1 - x^2}dt \\ dt &=& \frac{dx}{-\sqrt{1-x^2}} \end{eqnarray*} $

When $ t = 0 $, $ x = \cos 0 = 1 $
When $ t = \pi $, $ x = \cos \pi = 0 $

$ \begin{eqnarray*} & & \int\limits_{0}^{2\pi}{\sqrt{2 - 2\cos t}dt} \\ &=& 2\int\limits_{0}^{\pi}{\sqrt{2 - 2\cos t}dt} \\ &=& 2\int\limits_{1}^{-1}{\sqrt{2 - 2x}\frac{dx}{-\sqrt{1-x^2}}} \\ &=& 2\int\limits_{-1}^{1}{\sqrt{\frac{2 - 2x}{1-x^2}}dx} \\ &=& 2\sqrt{2}\int\limits_{-1}^{1}{\sqrt{\frac{1}{1 + x}}dx} \\ &=& 4\sqrt{2}\sqrt{1+x}|_{-1}^{1} \\ &=& 8 \\ \end{eqnarray*} $

Just as an aside, I used numerical integration and arc length approximation to make sure the answer is correct.

Differential Geometry of Curves and Surfaces - Chapter 1 Section 3 Exercise 1

Problem:

Solution:

The tangent line has direction $ \vec{a} = (3, 4t, 8t^2) $
The given line has parametric form $ (u, 0, u) $ so it's direction $ \vec{b} (1, 0, 1) $

The angle between these two direction is $ \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} = \frac{(3 + 8t^2)}{\sqrt{3^2 + (4t)^2 + (8t^2)^2}\sqrt{1^2 + 0^2 + 1^2}} = \frac{(3 + 8t^2)}{\sqrt{9 + 16t^2 + 64t^4}\sqrt{2}} = \frac{(3 + 8t^2)}{\sqrt{(3 + 8t^2)^2}\sqrt{2}} = \frac{1}{\sqrt{2}}$

So the angle is constant.

Differential Geometry of Curves and Surfaces - Chapter 1 Section 2 Exercise 5

Problem:

Solution:

$ |\alpha(t)| $ is a constant if and only if $ \alpha(t) \cdot \alpha(t) $ is a constant, so we focus on the latter, as a differentiable function of $ t $. Now it is differentiable and it is constant, then its derivative must be 0.

$ (\alpha(t) \cdot \alpha(t))' = 2 \alpha(t) \cdot \alpha'(t) $ so we know $ |\alpha(t)| $ is a constant if and only if the two vectors $ \alpha(t) $ and $ \alpha'(t) $ are orthogonal.

Differential Geometry of Curves and Surfaces - Chapter 1 Section 2 Exercise 4

Problem:

Solution:

Consider the function $ \alpha(t) \cdot v $, it is a differentiable function of $ t $, now $ (\alpha(t) \cdot v)' = 2\alpha'(t) \cdot v = 0 $ as the vectors are orthogonal. So $ \alpha(t) \cdot v $ is a constant function, and therefore $ \alpha(t) $ is orthogonal to $ v $ for all $ t $.

Differential Geometry of Curves and Surfaces - Chapter 1 Section 2 Exercise 3

Problem:

Solution:

Note that $ \alpha''(t) = 0 \implies \alpha'(t) = (a, b, c) $ is constant independent of t, so $ \alpha(t) = (at + x_0, bt + y_0, ct + z_0) $ is a straight line.

Differential Geometry of Curves and Surfaces - Chapter 1 Section 2 Exercise 2

Problem:

Solution:

The squared distance between $ \alpha(t) $ and the origin is $ \alpha(t) \cdot \alpha(t) $. It is a differentiable function of $ t $ and it reaches minimum at $ t_0 $, so $ (\alpha(t_0) \cdot \alpha(t_0))' = 0 $

Using the product rule, we get $ \alpha'(t_0) \cdot \alpha(t_0) = 0 $, now both vectors are non zero so they must be orthogonal.

Differential Geometry of Curves and Surfaces - Chapter 1 Section 2 Exercise 1

Problem:

Solution:

$ \alpha(t) = (\cos t, -\sin t) $.

Be careful with the clockwise direction.