Problem:
Solution:
This is a really bored after lunch hour, so I decided let's do a simple calculus exercise to wake my brain up.
The $ \frac{1}{1 + u^2} $ reminded me this has something to do with $ \tan $. So let's do this simple integration.
$ \int{\frac{du}{1+u^2}} = \int{\frac{\sec^2\theta d\theta}{1+\tan^2 \theta}} = \int{d\theta} = \theta = \tan^{-1}u $.
That's refresh my memory! $ \frac{1}{1 + u^2} $ is the derivative of $ \tan^{-1} u $.
Now we apply the Lagrange's mean value theorem to get:
$ \frac{\tan^{-1}v - \tan^{-1}u}{v - u} = \frac{1}{1 + \delta^2} $.
Where $ u < \delta < v $.
$ \tan^{-1}v - \tan^{-1}u= \frac{v - u}{1 + \delta^2} $.
Therefore we conclude (remember when you increase the denominator, the value decrease, and vice versa):
$ \frac{v-u}{1 + v^2} < \tan^{-1}v - \tan^{-1}u< \frac{v - u}{1 + u^2} $.
Last but not least, set $ u = 1 $ and $ v = \frac{4}{3} $ gives
$ \frac{\frac{4}{3}-1}{1 + \left(\frac{4}{3}\right)^2} < \tan^{-1}\frac{4}{3} - \tan^{-1}1< \frac{\frac{4}{3}-1}{1 + 1^2} $.
$ \frac{3}{25} < \tan^{-1}\frac{4}{3} - \tan^{-1}1< \frac{1}{6} $.
$ \frac{\pi}{4} + \frac{3}{25} < \tan^{-1}\frac{4}{3} < \frac{\pi}{4} + \frac{1}{6} $.
Solution:
This is a really bored after lunch hour, so I decided let's do a simple calculus exercise to wake my brain up.
The $ \frac{1}{1 + u^2} $ reminded me this has something to do with $ \tan $. So let's do this simple integration.
$ \int{\frac{du}{1+u^2}} = \int{\frac{\sec^2\theta d\theta}{1+\tan^2 \theta}} = \int{d\theta} = \theta = \tan^{-1}u $.
That's refresh my memory! $ \frac{1}{1 + u^2} $ is the derivative of $ \tan^{-1} u $.
Now we apply the Lagrange's mean value theorem to get:
$ \frac{\tan^{-1}v - \tan^{-1}u}{v - u} = \frac{1}{1 + \delta^2} $.
Where $ u < \delta < v $.
$ \tan^{-1}v - \tan^{-1}u= \frac{v - u}{1 + \delta^2} $.
Therefore we conclude (remember when you increase the denominator, the value decrease, and vice versa):
$ \frac{v-u}{1 + v^2} < \tan^{-1}v - \tan^{-1}u< \frac{v - u}{1 + u^2} $.
Last but not least, set $ u = 1 $ and $ v = \frac{4}{3} $ gives
$ \frac{\frac{4}{3}-1}{1 + \left(\frac{4}{3}\right)^2} < \tan^{-1}\frac{4}{3} - \tan^{-1}1< \frac{\frac{4}{3}-1}{1 + 1^2} $.
$ \frac{3}{25} < \tan^{-1}\frac{4}{3} - \tan^{-1}1< \frac{1}{6} $.
$ \frac{\pi}{4} + \frac{3}{25} < \tan^{-1}\frac{4}{3} < \frac{\pi}{4} + \frac{1}{6} $.
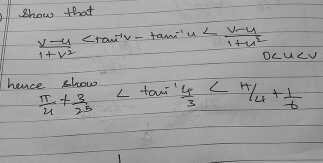
No comments:
Post a Comment